Broad approaches for situations of not-knowing
17/12/2023 ☼ not-knowing ☼ risk ☼ uncertainty ☼ strategy
This is the pre-reading for the 12th episode in a series of conversations exploring how to relate better to not-knowing.
tl;dr: A mindset for not-knowing helps us avoid sleepwalking into using the same old risk-based approaches for dealing with partial knowledge. Instead, this mindset brings clarity about the variety of non-risk types of not-knowing and how each type arises. This, in turn highlights how each type demands a different broad approach to taking action. These broad approaches are summarised in the figure below:
Different broad approaches for different types of not-knowing.
Mindset → Approaches → Tools
Why bother thinking about mindsets, approaches, and tools for not-knowing?
My reasoning is rooted in the problem we have faced so far: we choose tools for dealing with partial knowledge without considering whether the tools are appropriate for the work they must do.
To take only one example of such sleepwalking: consider how a risk assessment was unwisely chosen as a key decisionmaking tool in a situation that was truly uncertain.
In early 2020, the World Health Organisation used a “careful risk assessment” to make a poor decision in a situation of true uncertainty.
Risk assessments only work well for decisionmaking when what’s unknown is well-understood and accurately quantifiable — in other words, risk assessments are only appropriate as a decisionmaking tool when the partial knowledge situation is one of formal quantifiable risk.)
One antidote to this problem — the problem of sleepwalking into choosing inappropriate tools — is to be clear and explicit about beginning from a mindset for not-knowing, then moving to exploring approaches that are consistent with such a mindset, before finally identifying tools that fit with those approaches.
Mindset → Approaches
A mindset for not-knowing is essentially an explicit recognition that there are different types of not-knowing, only one of which is formal risk. (Read more on a mindset for not-knowing.)
This mindset explicitly recognises that there are types of not-knowing that are not risk — and that each type of not-knowing is conceptually distinct from the others. Not-knowing about actions is different from not-knowing about outcomes, about causation, and about values. Each type of not-knowing causes different problems for decisionmaking that must be dealt with differently.
Elimination
The next step is to consider what kinds of broad approaches are consistent with this mindset. A counter-intuitive but useful framing is to begin by asking what a mindset of not-knowing excludes from consideration. The simple answer is: Eliminated from consideration is any approach which assumes that i) all possible actions or outcomes are known in advance, ii) causation is known and stable, iii) relative valuation of outcomes is known and stable. Framed this way, all formal risk approaches (cost-benefit analyses, expected value calculations) are excluded.
Broad approaches consistent with a mindset for not-knowing
Not-knowing about actions
Not-knowing about actions emerges from uncertainty about the affordances (perceptible possibilities for action) of both new and existing technology (things that let us do stuff, including both physical objects and manipulations of ideas and objects). In essence, what this type of not-knowing highlights is that the space of possible actions is not fully understood — there are three types, shown in the table below. (Read more on not-knowing about actions.)
Sources of not-knowing about actions.
The broad approach for this type of not-knowing is to run many small experiments intentionally designed as a portfolio to explore the space of actions.1
These experiments are individually designed to evaluate whether an action is possible to take. “Experiment” here is loosely defined. An experiment can range from the completely conventionally recognisable (e.g. combining two reagents to see whether they form a novel polymer) to a plan of research on what actions have been taken in other similar or adjacent spaces (e.g., an educator studying the education system of a neighbouring country for new pedagogical actions).
The key parameters of this broad approach are multiplicity (many experiments are needed) and diversity (to cover more of the space of latent actions). Don’t place a small number of big bets — do a large number of small experiments. And actively design for diversity in the distribution and type experiments of experiments.
The intended result is a portfolio of experiments that collectively discloses new information about the space of actions: new actions that are possible, existing actions that can be redeployed, or existing actions that can be recontextualised. (Note that this portfolio investigative experimentation has a different logic from experiments designed to establish precise causation)
Conceptually, this broad approach could be partially analogised to Monte Carlo methods (since each experiment functions essentially as a deterministic computation with the result being informative about whether that action is possible and what affordances it allows).
Not-knowing about outcomes
Not-knowing about outcomes arises from the intersection of imagination and feasibility, as indicated in the quadrants of the diagram below. In essence, what this type of not-knowing highlights is that there is uncertainty (and thus potentiality) about what kinds of outcomes can be achieved. (Read more on not-knowing about outcomes.)
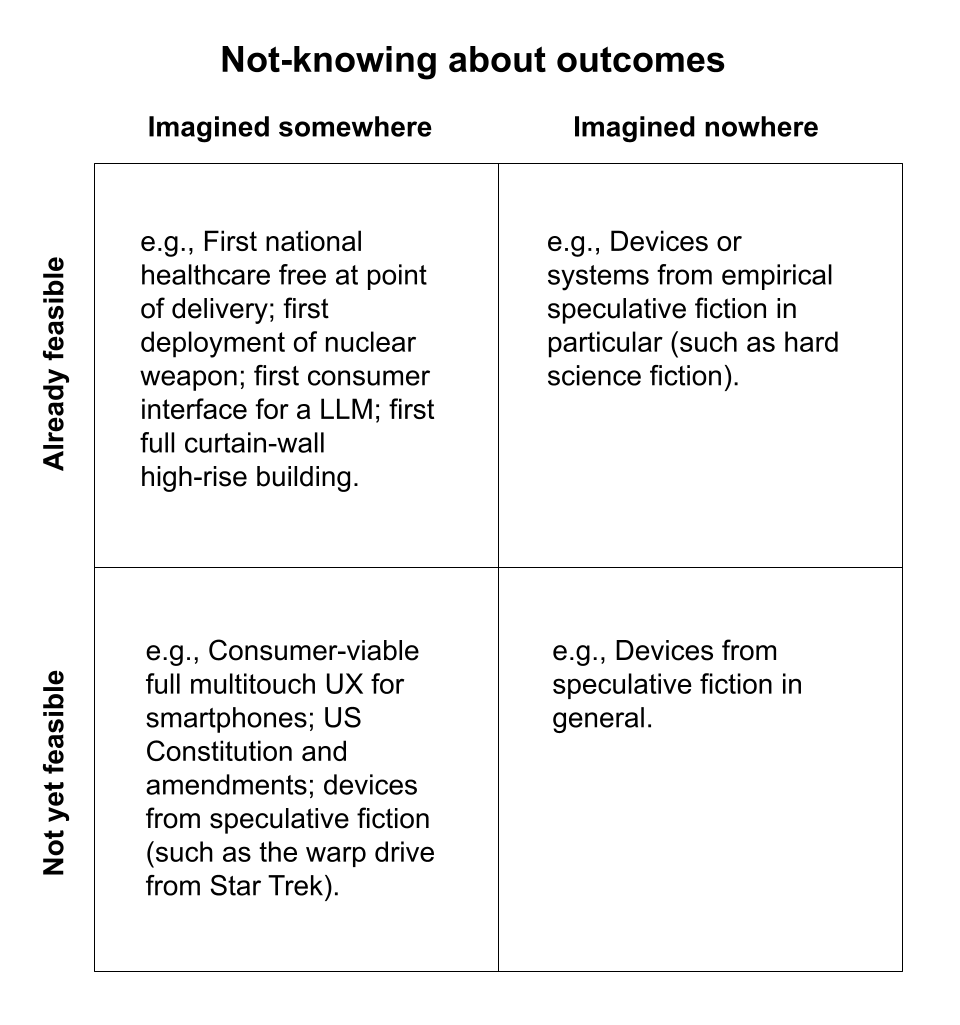Sources of not-knowing about outcomes.
For outcomes that are already-imagined, the broad approach is similar to that for not-knowing about actions: run many small experiments intentionally designed as a portfolio to explore the space of outcomes.
“Experiment” here is again loosely defined, but now the portfolio focus is on outcomes instead of actions. As an example, educators trying to reimagine their country’s education system might commission an experiment in the form of a qualitative study of culturally similar/different countries that specifically focuses on understanding differences in how countries define education outcomes.
For outcomes that are not-yet-imagined, the clearly appropriate broad approach is engaging in structured forms of exploratory imagination. This is much more easily understood as covering fiction (especially speculative fiction) and structured scenario planning (most famously, the Shell approach)
Causal not-knowing
Causal not-knowing is uncertainty about the precise connection between an outcome and the action/s that produce it. There are at least five types of causal not-knowing (illustrated in the figure below). The most straightforward type is when there is a stable causal link between an action A and an outcome X, but the probability of that causal link isn’t established yet — #1, where causal not-knowing can be resolved. The least straightforward type is where causation between action A and outcome X is inconsistent, in which case clear causation may never be possible — #5, where causal not-knowing is unresolvable.
Type #4 is generally closer to unresolvable not-knowing because multiple causation makes clear causal identification hard. Following the portfolio-level experimentation described in the previous two sections, #2 and #3 may be revealed to either be resolvable (this is the intended epistemological trajectory of a lot of academic research) or permanently unresolvable. (Read more on causal not-knowing.)
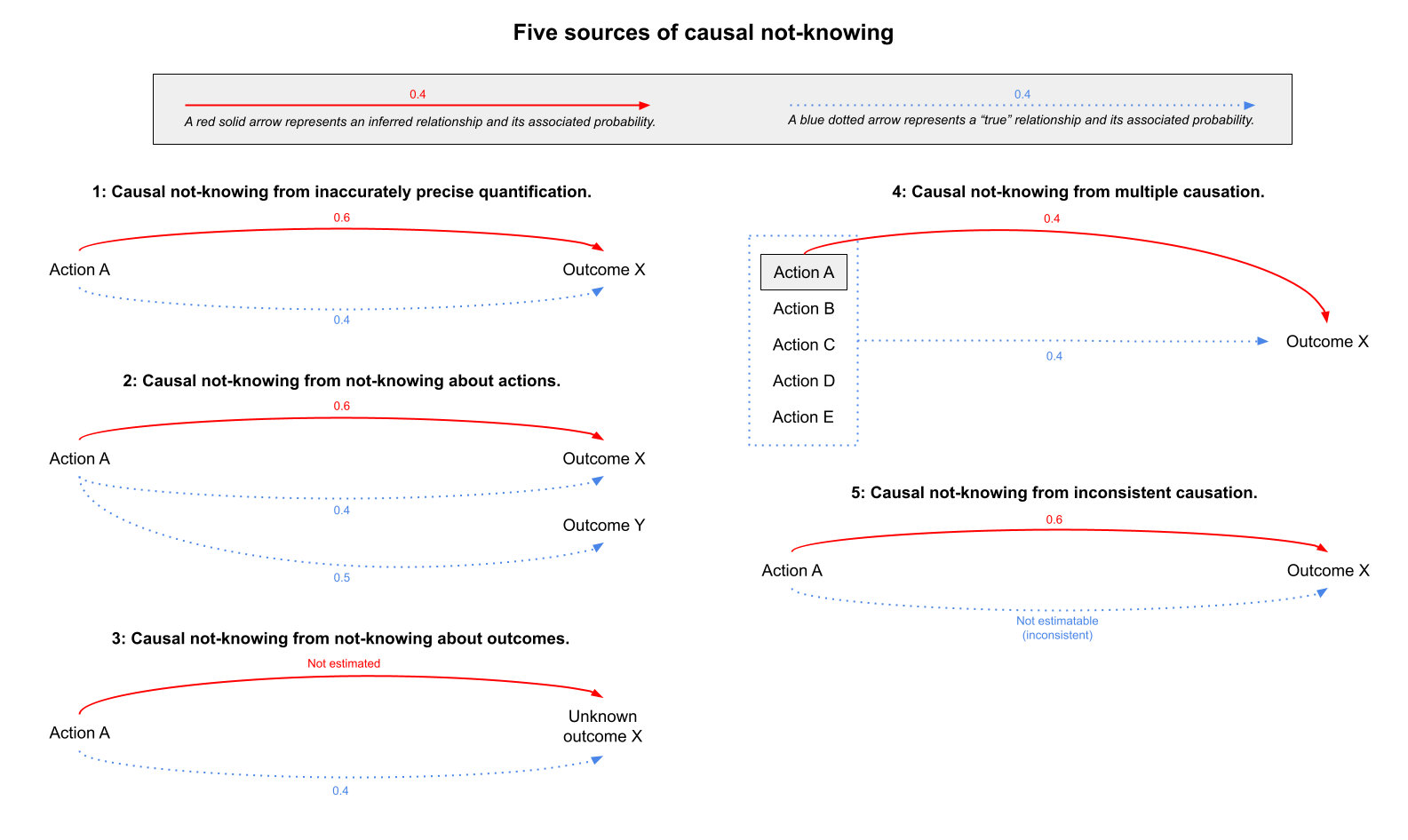Five sources of causal not-knowing.
For dealing with resolvable causal not-knowing, the broad approach to take is conventionally understood experimentation (well-structured hypothesis testing, including natural experimentation) — which is very well-understood. I’ve written a bit about what good hypotheses look like from a practical perspective.
But a lot of the really interesting causal not-knowing comes under the unresolvable category. This certainly seems to apply to most wicked problems. For unresolvable causal not-knowing, the broad approach to take is “stacking the deck.”2 This implies an approach to action that has two key characteristics: i) Doing many different small things (instead of a small number of big things), and ii) optimising for movement in a general direction (instead of movement in a specific direction).
Doing many small things (like doing many small experiments) makes sense because the causal effect of any one of the actions is unclear. When in doubt, do more things which are likely to have an effect. Why keep the individual actions small? Because this is the only way to limit the main downside of doing many things: serious unexpected side effects.
Optimising for general movement requires rethinking how to express goals, and particularly the level of abstraction with which goals are expressed. Specific directions map onto very concrete goals and success definitions (“sell $350k of new widgets by end Q2”), while general directions map onto more abstract expressions of goals that explicitly avoid defining success concretely and thus force ongoing meaningmaking (“we will be successful if we can sell enough widgets to validate our production system and cost estimates without losing money”).
Not-knowing about values
Not-knowing about values is uncertainty about how much a particular outcome is worth — where “value” is a subjective assessment. Not-knowing about value arises when the value of outcomes changes over time, is not fully known in advance, and/or differs among stakeholders. There are 5 types of not-knowing about value (listed in the diagram below).
Five sources of not-knowing about value.
Suitable approaches for not-knowing about value include reasoning/argumentation/negotiation/imagination about value and goal super-ordination.
Reasoning, argumentation, negotiation, and imagination address in different ways the subjectivity of valuation. Disciplines like philosophy (and particularly moral philosophy) are ultimately exercises in reasoning about value. Some kinds of speculative fiction engage in imagination about what should be valued and how much. And negotiation processes are ultimately attempts to converge on agreement about intersubjective value. Across these four ways of thinking about value, the commonality is articulating what the subjective value is (usually beginning from an explicit assumption that value is subjective in nature).
Goal super-ordination is a broad approach that is distinct from reasoning/argumentation/negotiation/imagination about value. In goal super-ordination, the idea is to define goals broadly enough (by going more abstract, hence super-ordination) that a broad range of value-definitions fit inside the definition (vs declaring and/or agreeing on a value-definition).
An example of goal super-ordination might be to define the goal as “selling enough widgets to validate our production system and cost estimates without losing money.” A potentially wide range of sales numbers, combined with other actions to influence production cost and other company financial parameters could be accommodated by this goal — which would be considered super-ordinated relative to the goal of “sell $350k of widgets.” The super-ordinated goal allows slightly different ideas of what is relatively valuable to co-exist within the company.
Different approaches for different types of not-knowing
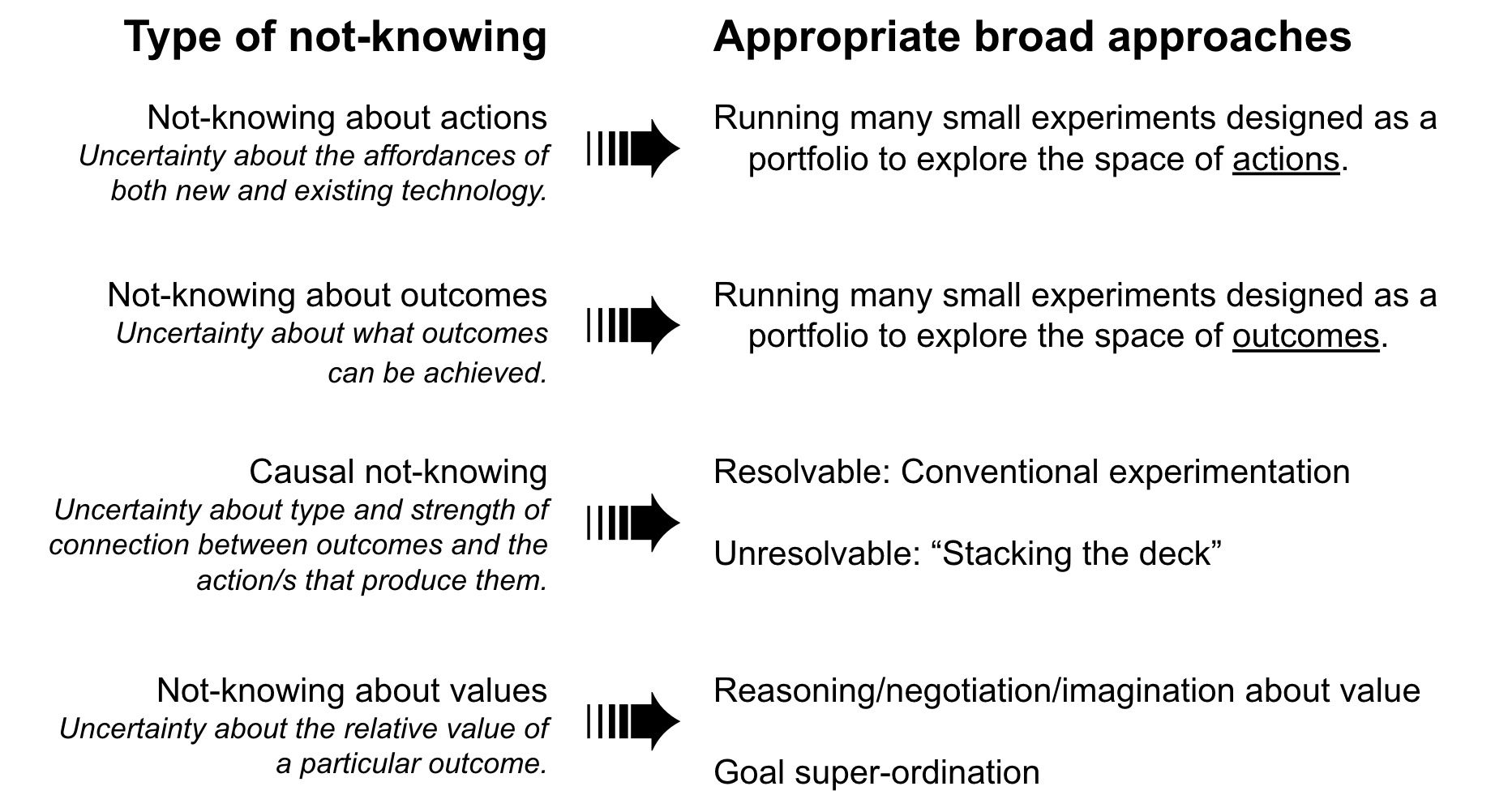Different broad approaches for different types of not-knowing.
The figure above summarises the relationships between the different types of not-knowing and the respective broad approaches for relating to them.
Being clear about the different types of not-knowing — and recognising where each type originates — highlights how a range of different broad approaches is necessary for relating well to the variety of not-knowing we routinely confront. Each of these broad approaches contains concrete tools that can become part of a toolkit for relating well to not-knowing; the next post will be about these type-specific tools.
Some new research also supports this view of using a portfolio of small experiments as a more optimal approach in fat-tailed distributions.↩︎
I’m borrowing and redeploying the phrase from Richard Hackman, who often talked about how many things would have to be done to move teams in the general direction of being more effective.↩︎