Causal not-knowing

4/7/2023 ☼ not-knowing ☼ risk ☼ uncertainty ☼ strategy

tl;dr: This post is about the five ways we might not-know about the relationships between actions and outcomes — in other words, five types of causal not-knowing. This is the reading for the seventh episode in my series of monthly discussions about not-knowing.

Pre-reading: This post builds on the previous instalment, which is about what it means to not-know about actions and about outcomes.

The usual caveat: Work in progress; may be only half-baked 🥖.

Why does understanding causal not-knowing matter?

Strategy is deciding what actions to take to get to desired outcomes. Causation is the connection between actions taken and the outcomes that result — an “if this action, then that outcome” relationship.

Making good strategy is impossible without knowing how particular actions are connected to particular outcomes. Strategy fails when we assume incorrectly that taking a particular set of actions will result in particular desired outcomes (while avoiding undesirable and unexpected outcomes). At the same time, causal not-knowing can also offer freedom to act under specific conditions and can create asymmetrical advantage in competition. Understanding causal not-knowing is a requirement for developing good strategy and for avoiding strategy failure.

In plain language, causal not-knowing is when we don’t fully understand the connections between specific actions and specific outcomes. Understanding causal not-knowing means untangling the different sources of not-knowing about causation.

Different types of causal not-knowing

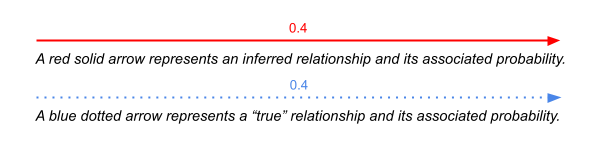
There are five sources and thus five types of not-knowing about causation:

1. Inaccurately precise quantification. 
2. Not-knowing about actions.
3. Not-knowing about outcomes. 
4. Multiple causation.
5. Inconsistent causation.

Five sources of causal not-knowing.

Each has a different path to resolution and thus offers different constraints and opportunities for planning and action.

In the diagrams that follow, red solid arrows indicate inferred causation while blue dotted arrows indicate “true” causation.

1: Causal not-knowing from inaccurately precise quantification

Our twin obsessions with quantifying things and making things legible makes us assign precise probabilities or probability ranges to known outcomes to make them fit into analytical frameworks (spreadsheets, cost-benefit analysis tables, etc). When the underlying mechanisms are regular and understandable and when we understand the boundary conditions of those mechanisms, our probability quantifications may be both precise and accurate.

However, when these mechanisms aren’t well understood, such precise probabilities are inevitably inaccurate. Note that this type of causal not-knowing comes not necessarily from the causal relationship itself but from our inability to accurately identify the probability of that causal relationship and the range in which that probability lies.

Example: Alex is an investment manager at a hedge fund. They’re evaluating a potential investment in litigation (i.e., investing in funding the costs of a lawsuit for a percent of the damages awarded if the lawsuit is successful) and presenting it to the fund’s investment committee for approval. The area of law the lawsuit pertains to is new, so there is little precedent to understand how likely the lawsuit is to be successful. There is therefore no way to accurately estimate the probability of the lawsuit’s success. Nonetheless. Alex must use the fund’s the standard investment comparison spreadsheet, which calls for a precisely bounded range for probability of success in order to calculate the range of potential costs and returns for this investment . Alex inserts this precise probability range, and the investment committee uses this completed spreadsheet as one of its bases for making a decision about whether or not to invest in this lawsuit.

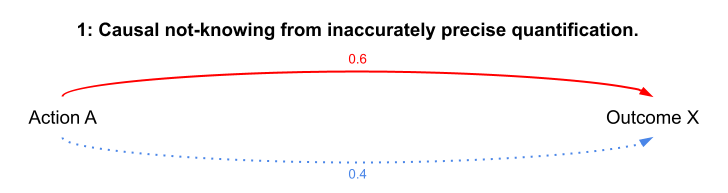Causal not-knowing from inaccurately precise quantification

Resolving this form of causal not-knowing requires investing in better measurement of the underlying causal mechanism.

2: Causal not-knowing from not-knowing about actions

Not-knowing about possible actions makes it harder to know how likely a given outcome is. Not-knowing about possible actions ultimately comes down to not knowing the full range of affordances (= possible actions) contained in any given technology (= things that enable actions, which includes both physical objects and manipulations of ideas and objects). An action taken with the intention of producing one particular outcome may thus have other unexpected outcomes (e.g., when a technology is new and its full range of affordances is not yet understood).

Example: Dichloro-diphenyl-trichloroethane or DDT is a chemical that was first synthesized in the late 19th century, then found to be an effective pesticide in the 1930s. DDT was originally deployed, with success, for controlling insects (like mosquitoes) that were transmission vectors for major diseases (like malaria). After several decades of widespread use, DDT was found to have other effects other than killing pesky insects. Because it resists breaking down into harmless components, DDT and its toxic breakdown products become more concentrated up the food chain especially in animal (and human) fatty tissue, have adverse effects on wildlife (e.g., harming bird populations by reducing egg viability), and potentially causes cancerous tumors in humans and other mammals. (Similar causal not-knowing dynamics at work in the slightly more recent 3M PFAS situation.)

DDT, a “Powerful Insecticide Harmless to Humans,” gets sprayed on beachgoers (!!!) in a 1945 photo. This image is from the Bettman Archive/Corbis.

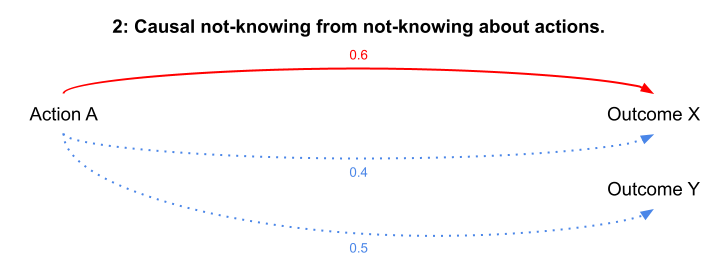Causal not-knowing from not-knowing about actions.

Resolving this form of causal not-knowing requires (in the first instance) investing in investigating the range of affordances (both desirable and undesirable) of any given technology.

3: Causal not-knowing from not-knowing about outcomes

Not-knowing about possible outcomes makes it hard to know which actions will produce them. When an outcome is unknown, you may not even think about what actions will produce them, let alone the precise relationship between that action and the unknown outcome. This is a conceptual inversion of Source 2 above.

Example: In 1940, telephony technology was limited to fixed-line systems with handsets physically connected to phone networks. The idea of full e-commerce and service platforms largely accessed through wirelessly-connected mobile devices through cellular phone towers was not a known outcome for which a set of actions and their respective causal probabilities could be constructed.

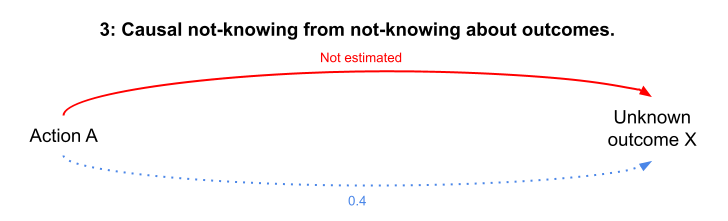Causal not-knowing from not-knowing about outcomes.

Resolving this form of causal not-knowing requires (in the first instance) investing in more diverse imagination about possible outcomes — e.g., through speculative fictions and imaginary ethnography.

4: Causal not-knowing from multiple causation

We are often only partly aware of the full set of causal connections between actions and a range of either simultaneously produced outcomes or sequentially revealed outcomes. A common situation is where many necessary but individually insufficient actions collectively result in an outcome — but causation for the outcome is attributed to only some of those actions. (This is a general problem with many historical and related approaches which focus on legible actions/events when interpreting causation. This may also be a form of causal not-knowing where our instinctive need for the comfort of clear causation is “resolved” with pointless rituals or cargo-cultism.)

Example: The emergence of innovation in high-end food is often attributed to individual highly creative chefs (such as Heston Blumenthal or Ferran Adria) creating restaurants which invested in R&D and produced continually changing menus. While the work these individual chefs/restaurants did was necessary, it was also insufficient. Other necessary but insufficient causes included the rise of new and different tastemakers in food, the emergence of online and offline chef networks (especially on social media), the creation of knowledge platforms focused on culinary innovation, and growing competition between chefs to be distinctive. (This is one of the topics in The Uncertainty Mindset)

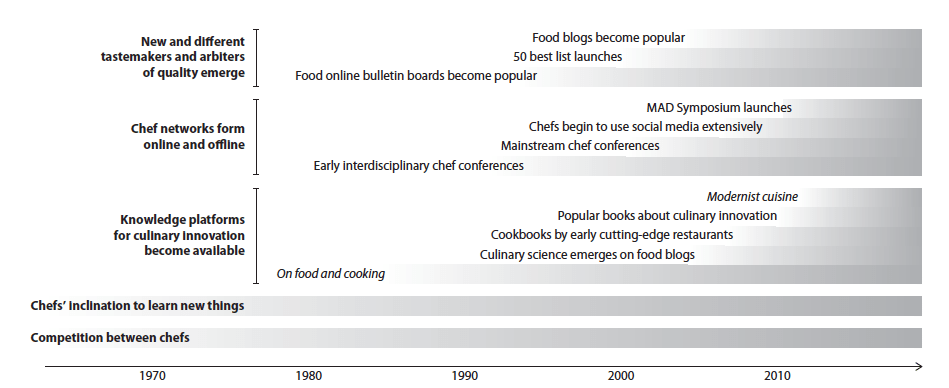Multiple causation in the emergence of a culture of innovation in high-end food.

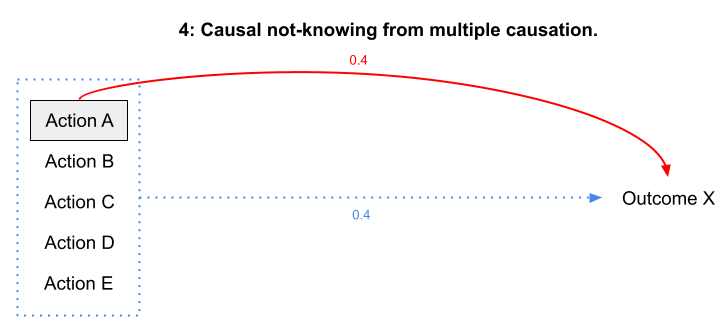Causal not-knowing from multiple causation.

Resolving this form of causal not-knowing requires investing in making and testing explicit inferences about causation.

5: Causal not-knowing from inconsistent causation

When a particular outcome is observed inconsistently or erratically, it is hard to figure out what action causes it in the first place (or whether a particular action causes it). This makes it hard or impossible to establish causation. Wicked problems seem to be afflicted by this form of causal not-knowing, though it occurs on much smaller scales as well.

Example: A piece of software crashes unpredictably and with no apparent pattern of actions leading up to failure — there isn’t yet a large enough pool of crash reports to extract a meaningful signal about what actions might be causing these crashes.

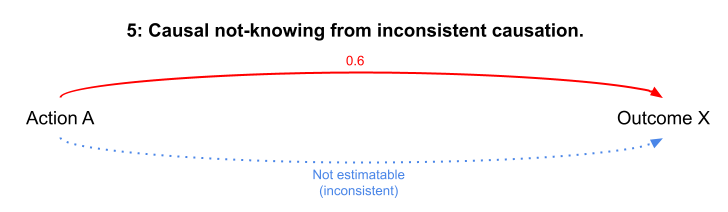Causal not-knowing from inconsistent causation.

Resolving this form of causal not-knowing requires first recognising it for what it is — this may require gathering more instances of the outcome and its possible antecedent actions or experiments designed to attempt replication of the outcome, with the understanding that resolution may be impossible.

Strategic benefits of causal not-knowing

Causal not-knowing can result in strategic advantage in two distinct ways:

1. Asymmetrical causal not-knowing: Causal not-knowing is asymmetrical when one party (e.g., a company or a country’s military) intentionally conceals or obfuscates its understanding of causation. Such asymmetry can prevent rivals (e.g., competing companies or other countries) from imitating a party’s success or lead rivals to over-invest in actions which have little or no effect on desired outcomes. Either way, the party creating the asymmetry in causal not-knowing gains strategic advantage from doing so.
2. Asymmetrical capacity to handle symmetrical causal not-knowing: When causal not-knowing is symmetrical (i.e., all parties experience the same degree of causal not-knowing), parties can still differ in their capacity to take action in resolving or acting under causal not-knowing. A party with this capacity will gain strategic advantage relative to parties lacking this capacity. (Such a capacity probably consists of people who are 1) not paralysed by causal not-knowing, 2) have a framework for understanding what kinds of not-knowing they face, and 3) have a toolkit of appropriate tools for use with different types of not-knowing.)